This gives a theoretical peak performance of 2.8 GFlop/s (vendor data and applied to
architecture) and a more
acceptable number of 600 MFlop/s (sum of performance of each physical processor,
data source: LinPack, Dongarra '95, applied to architecture).
One has to pay attention to these data because they only
represent a kind of overall performance. The machines were not dedicated to my job but also
to other users tasks.
Considering a parallel machine with S MFlop/s per node and minimum RAM transfer rate of M,
distributing loop2, so that each node computes a scalar-product of dimension n-k+1
we should be able to get data transfer rates over
With this set of 13 processors I tried out some benchmarks:
A scalar product like benchmark
Using N=20'000'000 iterations on a=b+c*d (where a,b,c,d are float type variables)
the following realistic specs for scalar floating point performance (SFPP) were obtained.
Scalar means that only one processor is used on a multiprocessor machine. First the time for the
loop and the assignment was measured (T0), then the full time including the floating point
operation (Tfp). The spec is computed as Flop/s=N/(Tfp-T0). The experiment was done
with real load (not exclusive).
machine
minimum
average performance
peak performance
Convex C-3220
10.20 MFlop/s
10.63 MFlop/s
10.84 MFlop/s
Convex C-3820
34.62 MFlop/s
36.34 MFlop/s
38.71 MFlop/s
Convex SPP-1000
-
32.41 MFlop/s
57.69 MFlop/s
HP 9000/715
18.18 MFlop/s
24.76 MFlop/s
55.56 MFlop/s
HP 9000/735
24.69 MFlop/s
32.82 MFlop/s
36.36 MFlop/s
IBM RS/6000-550
-
55.75 MFlop/s
136.36 MFlop/s
IBM RS/6000-591
142.86 MFlop/s
232.80 MFlop/s
666.67 MFlop/s
Mandelbrot set
By computing the iteration X[N+1]=X[N]^2+C and recording the speed of convergence
one get an image of the Mandelbrot set over the complex Gaussian area.
This computation was done in the interval [-1,1]x[-1i,1i] using up to 3200*3200 points.
Measuring the time to solution the following speedups were observed.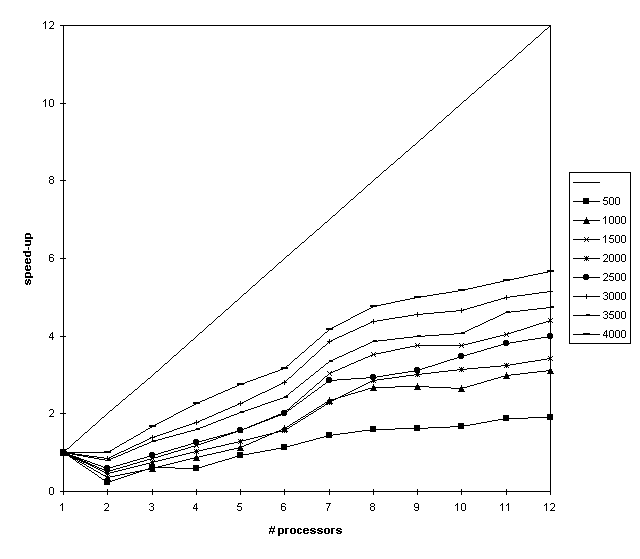
Gauss-Banachjewitsch linear equation solver
The algorithm for solving A*x=b is given by:
procedure swap(k,n)
- choose a line with index l>k but l<=n with abs(A[n,k])>=EPSILON
- if there is such line, exchange line k with line l
else terminate (A is singular)
for k:=1 to n-1 do begin { loop1 }
if (abs(A[k,k]) less EPSILON) then swap(k,n);
for i:=k+1 to n do begin { loop2 }
p:=A[i,k]/A[k,k];
for j:=k+1 to n do { loop3 }
A[i,j]:=A[i,j]-p*A[k,j];
b[i]:=b[i]-p*b[k];
end;
end;
for i:=n downto 1 do begin { loop4 }
x[i]:=b[i];
for j:=i+1 to n do { loop5 }
x[i]:=x[i]-A[i,j]*x[j];
x[i]:=x[i]/A[i,i];
end;
Because of dependency only the inner loops (loop2 and loop3) can be parallelised.
This leads to the following implication:
(3*(n-k+1)-1)*sizeof(float)
B >= ---------------------------
(2/S+4/M)*(n-k+1)
to be efficient (we have to send both the elimination line and the line to be computed).
When we have a sharp look at this formula we find out that we may identify the lower term
with the LINPACK benchmark.
|B| >= 12 * |LINPACK|
For our example this will require rates above 264 MByte/s. Taking an Ethernet-network with maximum
10 MBit/s=1.25 MByte/s peak rate into account we can state that it is inefficient in any case to
parallelise a Gauss-Banachjewitsch linear equation solver on a PVM cluster.
But it is possible to proof efficiency on the Convex Exemplar SPP-1000 because the CTI (the
Exemplar communication system) has raw data rates around 600 MByte/s, which might give a realistic
value of about 400 MByte/s.
Since what we discussed above is a scalar-product computation we can expand our conclusion to
all direct linear equation solvers which do not exploit the (sparse) structure of A.
Exploiting sparsity and/or matrix structure
If we can transform a given (sparse) matrix A into a block-diagonal structure we can
split the problem of solving a big linear equation system into several smaller independent
problems which can be solved parallel.
For better understanding the problem of sparsity some studies at
the ISC at the TU-Dresden should be
observed. We also want to reference to
"templates for the
solution of linear systems: Building blocks for iterative methods" (Barret et.al.).
Also have a look at the activities of
Top 500 Supercomputers
Supercomputers with vendor pages
SIMD (vector computer)
MIMD (real multiprocessor)
LAM/MPI homepage
Seymour Cray Memorial
![]()
![]() Department,
Department,
![]() Institute
Institute