Recently, in rotating nuclei a new type of symmetry breaking [1,2] was predicted which is called chiral symmetry breaking. This phenomenon appears in triaxially deformed nuclei if the direction of total angular momentum (a.m.) vector [J\vec] is outside all the three principal planes spanned by the intrinsic axes of the nuclear density distribution. The different principal axes form under those conditions either a left-handed or a right-handed intrinsic system with respect to the space-fixed vector [J\vec] which realizes two chiral symmetry types. In the ideal case two degenerate rotational bands appear corresponding to the chirally symmetric or antisymmetric intrinsic configuration with respect to the chiral operation c = T R_y(p) in which the rotation R_y(p) about the space-fixed y-axis is combined with time reversal operation T. Following the common phase conventions of [3] one gets straightforwardly for any tensor operators Q_lm the invariance property

c Qlm c-1 = Qlm.

(1)

The appropriate tool for describing these new features is the 3-dimensional Tilted Axis Cranking (TAC) model which enables us to calculate self-consistently the nuclear shape in conjunction with the off-plane orientation of the total spin which is crucial for obtaining chiral symmetry breaking. The 3d-TAC mean field Hamiltonian reads

h¢w(b,g)  =  ho -(h/2p)w° b ( cosg Q¢0 + sing (Q¢2+Q¢-2)/Ö2 )  - w (sinJcosj I1 + sinJsinj I2 + cosJ I3 ) (2)

where w is the rotational frequency, Q¢_0,±2 and I_1,2,3 denote the body-fixed components of the intrinsic quadrupole operator and a.m.vector, respectively. The angles (J,f) define the selfconsistent a.m.direction i.e. a minimum in the corresponding potential energy surface. The chiral symmetry breaking appears for 0 < J,f < p/2 which can only happen for a triaxial shape. In fig.1 such a situation is shown as calculated for the nucleus ¹³⁴Pr at the frequency (^h/_2p)w = 0.35 MeV.

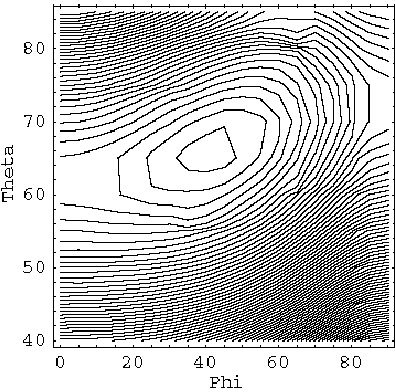
Fig. 1 Potential energy surface E(J,f) for ¹³⁴Pm which has a triaxial shape with g » 30^o.

In such a 3d-case the eigenfunctions |J,f > of h¢_w(b,g) become complex. The matrix elements of electromagnetic transitions can be calculated by projecting the wave function onto good chirality using the the relation

|± >   =   1 Ö2  (1 ± c) |J,f >  .

(3)

The label ± distinguishes the different chiral branches of the rotational DI = 1 bands. Evaluating the matrix elements of an electromagnetic operator M(l,m) by means of eq.(1) and for the complex TAC eigenstates one derives

< ±|M(l,m)|± >   = Âe( < J,f|M(l,m)|J,f > ),

(4)

< ±|M(l,m)|-± >   = Ám( < J,f|M(l,m),|J,f > )

(5)

Hence, the transition amplitudes within a given chiral branch (+ or -) and in between different branches can be expressed by the real and imaginary part of the complex matrix element. One should mention, however, that these simple relations are valid only when neglecting the possible overlap between chirally reflected states, i.e. < J,f|J,-f > = 0.

Experimental band structures measured in the isotonic chain at N=75 are shown in fig. 2 which are suggested to be candidates for chiral doublets |± > . The lowest pair of positive parity bands in ¹³⁴Pr has been interpreted as a chiral doublet in [1,2]. New measurements at GAMMASPHERE extended the doublet seen for large frequency up to w = 0.6 MeV [4]. In order to exclude an accidental degeneracy the neighboring nuclei have been studied [5]. The systematic appearance of low-lying doublet bands of the same parity in the N=75 isotones with the disappearance of the energy difference in ¹³⁴Pr makes it likely that a small island of chiral rotation has been found which is surrounded by shores of soft chiral vibrations as is the case for other islands of broken symmetries, such as with quadrupole deformation, octupole deformation, and now rotational chirality. Clearly it would be interesting to study the neighboring isotone chains in order to map out the complete island.

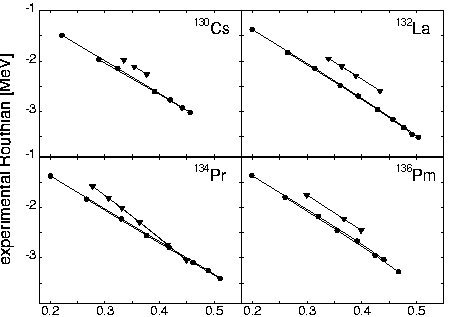
Fig. 2 Experimental Routhians for the ph_11/2nh_11/2 main band (circles) and side bands (triangles) in the N=75 isotones studied. The Routhians are plotted up to a spin of I+11, where I is the bandhead spin. The distance between the two bands is the frequency of the chiral vibration. From [5].

¹ Department of Physics and Astronomy, University of Tennessee, TN 37996, USA
² on leave of absence at the Faculty of Physics, University of Notre Dame, IN 46556, USA
³ Faculty of Physics, Sofia University, 1164 Sofia, Bulgaria

References
[1] S. Frauendorf and J. Meng, Nucl. Phys. A 617, 131 (1997)
[2]V.I. Dimitrov, S. Frauendorf and F. Dönau, Phys. Rev. Lett. 84, 5732 (2000)
[3] A. Bohr and B.R. Mottelson, Nuclear Structure I, Benjamin, New York, 1969
[4] D. Fossan, private communication
[5] K. Starosta et al., Phys. Rev. Lett. 86, 971 (2001)  IKH 06/20/01 © F. Dönau