Power buildup
Switching on the electron beam the undulator spontaneously starts to emit radiation with a wavelength around the resonance wavelength λn. The intensity Ispont of this spontaneous emission is by roughly 6 orders of magnitude smaller than the asymptotic laser intensity. After reflecting the electromagnetic wave at the two mirrors of the optical resonator it interacts with the subsequent electron pulse and is amplified by a factor 1+GN, where GN is the single-pass gain of the N-th roundtrip. At the beginning the gain Gn is identical to the small-signal gain. When the laser intensity increases the gain reduces by the saturation factor ηNsat(IN), which depends on the ratio of the current intensity IN in the N-th roundtrip to the saturation intensity Isat according to
ηNsat(IN)=[1+IN/Isat-0.14IN/Isat(1-IN/Isat)]-1.
The saturation intensity describes that intensity at which the actual gain is half as large as the initial small-signal gain. It depends on undulator and electron parameters [2].
While the gain increases the intensity it is reduced by the outcoupling of a fraction A and by diffraction and reflection losses V. Altogether the intensity IN+1 after N+1 roundtrips can be related to the intensity IN of the N-th roundtrip by
IN+1 = (1+GN)(1-V-A) IN+Ispont .
After a few roundtrips the spontaneous contribution Ispont is negligible. As long as the gain GN is larger than the total losses V+A and the intensity IN of the radiation is much smaller than the saturation intensity Isat the intensity grows exponentionally. If the laser intensity comes close to the saturation intensity the gain is reduced until it reaches a value which just compensates the total losses V+A. From now on the intensity remains constant at its asymptotic value.
The temporal behaviour of the FEL is illustrated in the figure below. It shows the evolution of the gain and of the intra-cavity and outcoupled intensity calculated for different outcoupled fractions.
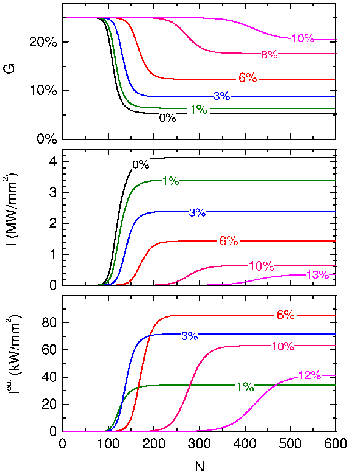 |
The evolution of the single-pass gain G (upper plot), the intra-cavity intensity I (center plot) and of the outcoupled intensity Iout (lower plot) is shown as a function of the number N of roundtrips calculated for different output couplers. The small-signal gain was assumed to be 25% and the saturation intensity was fixed to 140 MW/cm2. 5% losses were assumed. The intensities considered here are peak intensities. Average intensities are obtained by multiplication with the micropulse duty-cycle of ≈3×10-5 for 1 ps pulses (rms) at ELBE. Approximately after 100 roundtrips the beam intensity exceeds a noticeable value. The larger the outcoupled fraction the more trips are necessary to reach that level. Approaching to the saturation intensity Isat the gain starts to decrease (upper plot) until an asymptotic value is reached which is given by the sum V+A. From this value on gain and intensity are constant. The larger the sum of losses and outcoupled fraction the lower is the asymptotic intensity in the resonator. The outcoupled part of this intensity (lower plot) has an optimum value Aopt at a definite outcoupling fraction (≈6% in the figure). Smaller and larger outcoupled fractions result in a lower outcoupled intensity. When the sum V+A exceeds the small-signal gain the intensity does not start growing. In this case, only spontaneous emission is observed. The optimal output coupling depends on the small-signal gain G and on the resonator losses V. It varies for the undulators of ELBE between 1 and 8%. |
Constant values of small-signal gain, losses and outcoupled fraction describe an idealized behaviour. In reality, they may vary from one round-trip to the next even in a rather discontinuous manner. In that case the intensity may still vary in the asymptotic region.
[2] G.Dattoli, A.Renieri and A.Torre, Lectures on Free-Electron Laser Theory and Related Topics, (World Scientific, Singapore, 1993); G.Dattoli, L.Gianessi and A.Torre, Phys.Rev.E48 (1993) 1401-1403

