X-ray reflectometry (XRR)
The scattering geometry of an incident plane wave is scetched in Fig.1 and Fig.2.
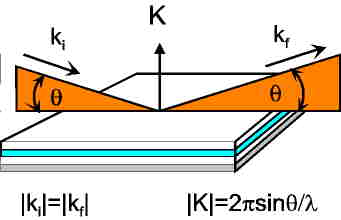 |
| Fig. 1 Scattering geometry of XRR |
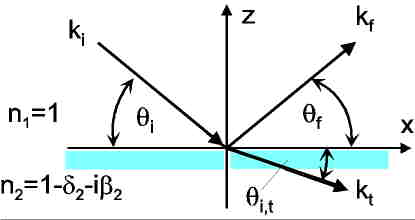 |
| Fig. 2 Reflection and transmission at a plane surface |
Because the refractive index of X-rays n differs for matter only by small amounts(e.g., δ ~ 10-5, β ~ 10-6) from the vacuum value (n0=1), n = 1 - δ - iβ, and |n|<1, total extrernal reflection occurs for incident angles αi smaller than the critical angle αc. The critical angle is (for β << δ)
αc ~ (2δ)1/2~Z (Z - atomic number)
The critical angle of total external reflection is small (~0.2°- 1° for a wavelength λ of ~ 0.1 nm) and interferences from thin films are only visible in a small range close to the critical angle.
Reflectometry is sensitive to the electron density and absorption and does not depend on crystallinity and crystal texture. The reflected intensity RF is given by the known Fresnel equations. Fig.3 shows the RF of a perfect Si-vacuum interface.
| Fig. 3 Reflectivity of a perfect Si-vacuum interface for different values of absorption and a wavelength of l =0.154nm |
- For αi << αC and β >> 0 --> R = 1
(total reflection)
- For αi > αc --> RF ~ Kz-4
RF ~ αi-4
| Fig. 4 In some cases the surface roughness σrms can be described as a Gaussian distribution of the height h of the hills and valleys around a average surface level h0 |
-
Surface roughness σrms is introduced by a Debye-Waller factor
-
RFrough = RF exp(-Kz2σrms2)
-
if the height distribution is Gaussian-like as shown in Fig.4.
XRR on thin films and Multilayers
The reflected intensity may be calculated using a recurrence formalism which calculates the reflection coefficient starting from the lowest surface boundary (substrate) up to the last (surface / air).
With a code (based on the Parratt or matrix formalism) a simulation of XRR spectra can be done. The parameters film thickness (d), density (ρ) and roughness (σrms) can be exctracted from the interference spectra, the critical angle, and the decrease of the reflectivity as schematically shown in Fig.5 for a Ta layer on silicon substrate.
| Fig. 5 Specular reflectivity of an oxidized Ta layer deposited on a Si-wafer (measured at ROBL with a wavelength of l=0.1033 nm) |
Experimental setup for XRR
The Figs. 6 and 7 show the diffractometer D5000 (SIEMENS) in theta-theta geometry with the special cutting slit device for reflecometry. The divergent beam of a sealed copper tube is matched into a parallel beam by a Göbel mirror. With such a beam the cutting slit may have a larger slit width and furthermore in the most cases one does not need a collimator-analyzer device. The gain in intensity reduces the measuring time for specular scans extended to higher incidence angles. This is of special interest for the study of multilayers.
XRR is non-destructive technique and can be used for samples with a sufficently smooth surface.
| Fig. 6 Scheme of experimental setup |
|
Fig. 7 D5000 (SIEMENS) in theta-theta geometry with Göbel mirror and cutting slit device.
|

